Difference between sort and sorted functions in Python
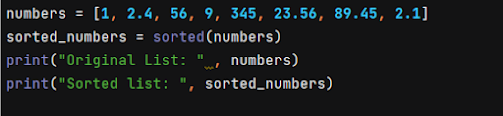
Why Sort Lists? We often need to sort the elements of a list for various reasons like searching for elements, merging elements, optimizing list performance and readability etc. In Python we can use 'sort' and 'sorted' functions to sort a list. While both functions can be used to sort a list there are some differences in the usage of these functions that should be kept in mind before using one over the other. Sorted Sorted function (built-in) takes a list as argument (along with other optional arguments) and returns a new list with elements of original list sorted in ascending or descending order. Output: To sort the list in descending order, add reverse = True with the list argument. Output: Sort Sort function/ method will sort the original list without the need of creating a new list. It is applied on the list object rather than taking the list as an argument. Output: Keep in mind that you should not assign the sort fun...
